
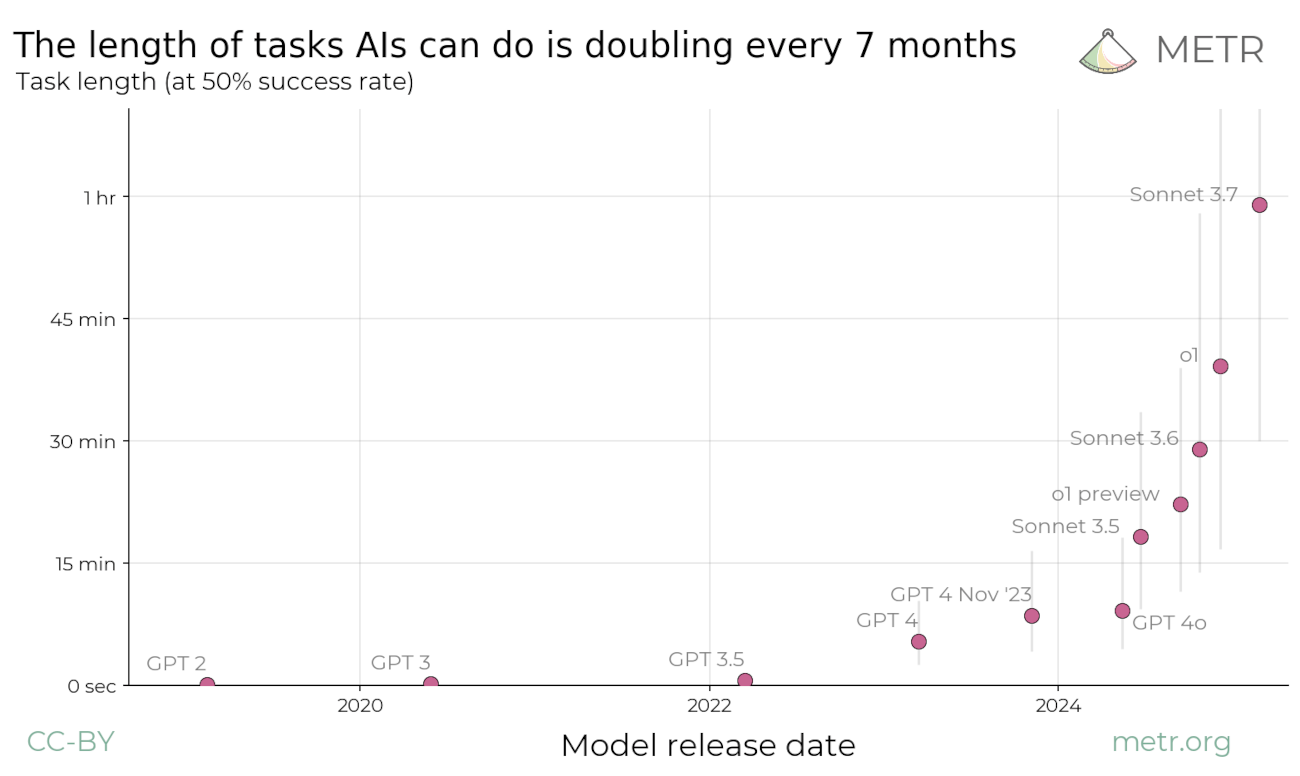
METR measures how long frontier AI agents can work autonomously before their success rate degrades. Their task horizon has doubled roughly every seven months since 2019, providing a grounded baseline that replaces guesswork about capability curves.
On each page load, the calculator pulls the full METR benchmark dataset and identifies the latest state-of-the-art model (currently GPT-5.1-Codex-Max, November 2025) as the capability baseline. It computes the doubling time dynamically via linear regression across all historical SOTA models, so the trend reflects actual measured progress rather than a hardcoded assumption. Your current date serves as the projection starting point.
For example, GPT-5.1-Codex-Max shows a 50th percentile task horizon of ~162 minutes and an 80% success horizon of ~31 minutes. We fit a logistic success curve through these measurements. At the default 95% reliability requirement, the effective horizon contracts significantly (about 33× shorter than the median). A 99% requirement would shrink it further (~235× shorter).
- Doubling trend: Computed dynamically from METR data via linear regression (typically ~6-7 months). The calculator fits log2(p50) against time across all SOTA models to derive the current doubling rate.
- Reliability gate: We require 95% success before automation kicks in. Technical capability requires a high bar to outperform human error, though you can adjust this threshold in the calculator.
- Task mapping: Your job gets decomposed into five task duration buckets: [5, 30, 120, 360, 720] minutes (roughly <10 min, 10-45 min, 45 min-3 hr, 3-8 hr, and >12 hr tasks). These thresholds are calibrated for corporate production work. Once AI can reliably complete enough of these categories, the hazard channel opens.
- Scenario levers: Industry-specific friction and required reliability, plus your questionnaire responses, adjust capability. The doubling time is computed from historical data but can be overridden in Advanced Model Tuning. Friction multiplies the horizon penalty (p_domain); reliability tightens the success bar.
What the calculator actually simulates
The calculator models job displacement as a survival problem with multiple compounding hazard channels. A complete model would include macroeconomic forces, firm performance, layoffs, and other non-AI risks, but this calculator focuses solely on AI-related hazards at the role, personal, and firm levels. Treat the output as one component of your total displacement risk, not the whole picture.
The AI hazard rate ($\lambda_{\text{AI}}(s)$) determines the blue technical feasibility curve. Your firm and personal questionnaire responses then shift this curve forward in time and add a compression hazard channel to create the green implementation curve. The same data also determines your re-employment probability.
- AI hazard (blue curve): METR task-length data map capability progress into technical feasibility.
- Compression hazard (green curve only): Workforce reductions via task reallocation to AI-amplified seniors, activated at lower capability thresholds for vulnerable hierarchy positions.
- Implementation delay (green curve): Firm and personal answers shift the AI automation hazard forward in time.
- Re-employment likelihood: Adaptability and transferable skill questions translate into the percentage you see on the dashboard.
Model Flow: How Your Inputs Become Predictions
Model Defaults
Friction Decay Parameter
The model tracks how quickly organizational barriers erode over time using a decay rate (λ). This parameter is calculated from your questionnaire responses about company adoption readiness, infrastructure, labor market dynamics, and role characteristics:
where $n_i$ is the normalized answer to question $i$ (Likert 1-5 scaled to 0-1), and $\lambda$ is clamped to $[0.005, 0.05]$
This parameter controls how quickly implementation barriers diminish as AI capability grows. The model implements dynamic friction decay where implementation delay decreases exponentially: $\Delta(t) = \Delta_0 \cdot e^{-\lambda t}$. At time $t$, the green curve (actual job loss) equals technical feasibility at the earlier time $t - \Delta(t)$. Higher $\lambda$ means barriers collapse faster once AI crosses initial thresholds; lower $\lambda$ means barriers persist even as capability advances. This captures how regulatory frameworks and organizational inertia may initially delay adoption by several years, but these delays shrink as AI becomes more capable and widespread adoption creates network effects.
Role Presets
Different roles face different automation barriers. Software engineering maps most directly to AI's training data and requires less physical presence, so it gets lower friction (1.05x). Legal work and traditional engineering involve more tacit knowledge, regulatory constraints, and liability concerns, earning higher friction multipliers (1.45–1.50x). These multipliers reflect how much harder it is to automate each domain compared to software.
Two-layer friction system: The model applies friction at two layers: industry and role. The industry slider affects all roles in a sector (finance 1.35× applies to analysts, controllers, and auditors alike). Your questionnaire responses then add role-specific friction based on tacit knowledge, physical presence, and context dependencies. Both layers multiply together, so a high-context legal role in a regulated industry faces compounded barriers.
- Domain friction (preset baseline): Role presets set an initial friction multiplier (software ~1.05x, admin/data ~1.10x, finance/consulting ~1.35x, legal ~1.45x, engineering ~1.50x) before individual job characteristics are considered.
- Recommended reliability: Presets suggest a reliability starting point per role based on typical error tolerance and stakes (finance/legal 97–98%, software/data 92–93%, creative/customer service 88–90%). Seniority adjusts these baselines: entry-level roles tolerate slightly lower reliability (−0.05), while executive decisions demand higher confidence (+0.05). Higher reliability requirements significantly reduce effective task horizon. You can override both friction and reliability in the UI to test different scenarios.
Beyond the preset baseline, the calculator derives a role-specific domain alignment penalty from your answers. Digitized, decomposable, and standardized work (Q4/Q5/Q6 high) reduces the penalty; context dependence, tacit knowledge, judgment/relationship load, and physical presence (Q7/Q9/Q11/Q12 high) increase it. The model forms a signed weighted sum and maps it to a penalty multiplier via an exponential, clamped to a reasonable range. This penalty multiplies with the sector slider, so misalignment compounds friction.
The hazard activates once AI capability crosses a coverage threshold. Two gates control this: task-level gates determine which individual tasks AI can handle, while a job-level gate opens when enough of your job is automatable to justify replacement. Here's the sequence:
- Task-level gates open gradually: As AI capability $H_r(t)$ grows via METR's doubling trend, each task bucket's gate $G_i(H)$ opens. Short tasks automate first (gates open when $H$ exceeds their threshold $L_i$), then medium tasks, then long tasks. Your personalized weights $w_i$ determine how much each gate contributes to overall readiness.
- Job readiness accumulates: $A(t) = \sum w_i G_i(H)$ sums up all the open gates, weighted by your job profile. This gives a number between 0 and 1 representing what fraction of your job AI can perform.
- Job-level hazard gate activates: When $A(t)$ crosses the coverage threshold $\theta$ (typically 0.50), the hazard function $\lambda_{\text{AI}}(t)$ rapidly increases via the logistic gate. Before this point, hazard is near zero; after, it approaches the maximum $h_{\max} \times M_{\text{user}}$.
where $p_{\text{domain}}$ = role-specific penalty from questionnaire, $f_{\text{industry}}$ = industry friction slider
Automation doesn't happen all at once. AI steadily masters more of your tasks (task gates opening), but job displacement risk only spikes once AI can handle enough of your role to justify replacement (job gate opening). Jobs with more long-duration tasks take longer to reach this threshold.
- Task horizon $H_r(t)$: $$H_r(t) = \frac{H_{50,0} \cdot 2^{(t \cdot 12)/D}}{p_{\text{domain}} \cdot f_{\text{industry}} \cdot f(r)}$$ where $D$ is METR's doubling period (computed dynamically from benchmark data, typically ~6-7 months). The baseline capability $H_{50,0}$ is divided by domain and industry friction penalties (described above), which reduce AI's effective capability for roles that are harder to automate. $f(r)$ is the reliability factor: higher reliability requirements further divide $H$, reducing AI's effective maximum task length. At the default 95% reliability, $f(0.95) \approx 33.4$, contracting the 50th percentile horizon (~162 min) down to about 4.8 minutes for production use.
- Personalized task weights $w_i$: Your answers to Q5 (task decomposability), Q6 (task standardization), Q7 (context dependency), and your hierarchy level determine how your job breaks down across the five buckets. Entry-level roles skew toward shorter tasks; executive roles skew toward longer tasks. Highly structured jobs concentrate weight in the short buckets; complex jobs shift weight to longer buckets. High-context work means more weight in the 1–3 hr and >12 hr buckets. The weights always sum to 1.0 and represent what fraction of your job falls into each duration category.
- Gate softness parameter $s$: Controls how sharply tasks transition from "AI can't do this" to "AI can do this". Entry-level structured work has sharper transitions; senior complex work has smoother, more gradual automation curves. Base value is 0.35, adjusted by seniority (±0.03 per level) and task complexity (Q5, Q6). Range: [0.20, 0.55].
- Readiness $A_{\text{job}}(t)$: $$A_{\text{job}}(t) = \sum_i w_i G_i(H_r(t))$$ This weighted sum tells us what fraction of your job AI can perform at time $t$. If you're an entry-level role with 40% of tasks under 5 minutes and AI's capability $H_r(t)$ has reached 10 minutes, the <5 min gate is fully open ($G_1 \approx 1.0$), contributing $0.40 \times 1.0 = 0.40$ to readiness. Jobs with more long-duration tasks need higher $H_r$ before their readiness $A(t)$ crosses the coverage threshold $\theta$, delaying automation.
- Coverage bar $\theta$: Baseline is 0.50, adjusted by seniority (thetaLift from -0.02 to +0.08), domain alignment (±0.12), and role explicitness (±0.10). Data-rich jobs, standardized workflows, and fast feedback loops lower this threshold because automation becomes viable earlier. Conversely, tacit knowledge, high context, and senior roles push it higher. Clamped to range [0.50, 0.85]. This threshold controls how much of the job must be automatable before displacement risk activates.
- User multipliers $M_{\text{user}}(s)$: Questionnaire responses exponentiate into amplifier and friction sums, then are capped between $0.33\times$ and $3\times$ for responsiveness.
How your answers move the curve
Your answers are converted to a scale where neutral (3) = 0, allowing symmetric effects. The model combines these into amplifier and friction scores, then converts them to multipliers ranging from 0.33× to 3.0×.
The prompts fall into four themes:
- AI readiness (Q1-Q4): High scores strengthen the amplifier channel when you indicate strong capability for AI learning and completing your tasks. Additionally, Q1 (current AI performance), Q2 (example work availability), Q3 (benchmark clarity), and Q4 (work digitization) all contribute to role explicitness ($s_e$), which lowers the coverage threshold $\theta$, making automation viable at lower overall capability levels.
- Task structure (Q5–Q9): These questions affect the blue curve (technical feasibility) through multiple mechanisms: (1) Q5, Q6 shift the task duration profile (structured → shorter buckets, complex → longer buckets), (2) Q2, Q5, Q6, Q8 contribute to $s_e$ which lowers $\theta$ (data-rich, decomposable, standardized, fast-feedback jobs become viable at lower capability), and (3) Q7, Q9 increase the domain penalty $p_{\text{domain}}$ (high context, tacit knowledge damp capability). Together, these determine when your specific job crosses the automation threshold.
- Human moat (Q11-Q12): Relationship intensity and physical presence both load the friction side and stretch the METR baseline via the domain penalty, pushing the curve out.
- Firm and personal context (Q13-Q19): Company levers shape implementation delay. Job performance (Q19) delays displacement for top performers while also helping re-employment. Adaptability (Q18) and transferability (Q17) drive re-employment probability.
How role clarity affects the threshold: Questions Q1, Q2, Q3, Q4, Q5, Q6, and Q8 (positive factors) are averaged together, while Q7 and Q9 (context dependency and tacit knowledge, the protective factors) are averaged separately. The formula $s_e = 0.65 \times \text{norm}(s_{\text{pos}}) - 0.35 \times \text{norm}(s_{\text{neg}}) + 0.10$ produces a score between 0 and 1. Higher scores (more explicit roles) reduce $\theta$ via the shift $\Delta_{s_e} = 0.10 \times (0.5 - s_e)$, meaning AI needs less total job coverage before automation becomes economically viable.
The model also adjusts the gate steepness $\gamma$ based on task characteristics. Structured work, fast feedback, and standardized tasks sharpen the S-curve; messy, collaborative, or bespoke work flattens it. This captures whether adoption snaps into place once the threshold is crossed or grinds along for years.
The green curve: Implementation delay and workforce compression
The green curve (actual job loss) differs from the blue curve (technical feasibility) through two mechanisms. The blue curve shows when AI can do the job technically. The green curve shows when job loss actually occurs, accounting for organizational adoption barriers and earlier compression-driven workforce reductions.
How the green curve is calculated
The model integrates two separate hazard channels to create the green curve:
This structure captures two different ways jobs disappear:
- Delayed automation hazard: The AI automation hazard $\lambda_{\text{AI}}$ is evaluated at an earlier time $(t - \Delta(t))$ due to organizational friction. Early in the timeline, implementation barriers create a significant delay ($\Delta_0$), but this delay shrinks exponentially as AI capability grows and adoption accelerates. The friction decay rate $\lambda$ determines how fast these barriers collapse.
- Compression hazard: A separate hazard channel $\lambda_{\text{compression}}(t)$ that activates when AI makes senior workers productive enough to absorb junior work. This hazard is evaluated at the current time $t$ (no delay) and can cause job loss well before full automation becomes technically feasible. The two hazards are summed and capped at 0.60/year total.
Mechanism 1: Implementation delay (shifts automation hazard forward)
Organizational barriers slow AI automation adoption. The initial delay $\Delta_0$ derives from company context (Q13-Q16: adoption appetite, labor cost pressure, market tightness, infrastructure) and individual leverage (Q19: job performance protects top performers). This delay ranges from 0.3 to 4.0 years depending on your situation.
$s_{\text{delay}} \in [-2,2]$ from Q13-Q16; $\Delta_{\text{seniority}} \in \{-0.25,-0.05,+0.10,+0.20,+0.30\}$ by level
Dynamic friction decay: The delay doesn't stay constant. As AI capability increases and adoption spreads, organizational barriers erode exponentially: $\Delta(t) = \Delta_0 \cdot e^{-\lambda t}$. The decay rate $\lambda$ (typically 0.02-0.05/year) is inferred from your answers about adoption readiness, infrastructure, and role characteristics. Higher $\lambda$ means barriers collapse faster once AI crosses initial thresholds; lower $\lambda$ means delays persist even as capability advances.
Example delays: An early-adopting entry-level role starts with a 0.3-year delay. A defensive environment with senior leadership starts with a 4.0-year delay. Performance (Q19) adjusts these: high performers get extended delays; low performers face shortened timelines.
Mechanism 2: Workforce compression (earlier job loss via task reallocation)
Jobs can be eliminated well before AI reaches full automation capability. When AI makes senior workers more productive, companies can reduce headcount by redistributing work upward in the hierarchy. An entry-level software engineer's role might disappear when AI can only handle 35% of their tasks. Not because AI does everything, but because AI-amplified senior engineers can absorb the remaining 65%.
The compression hazard activates earlier and at a lower threshold than full automation. It depends on three factors:
The hybrid formula means compression readiness has two components: 70% comes from reallocation feasibility alone (immediate effect), and 30% grows over time as AI amplifies senior productivity. This ensures Q10 has a noticeable immediate impact while preserving the time-dependent behavior where compression risk accelerates as AI becomes more capable.
- Reallocation feasibility ($s_{\text{realloc}}$): Combines Q10 (direct reallocation question: 50% weight), task structure (Q5: 18%, Q6: 12%, Q7: 8% inverted), tacit knowledge (Q9: 10% inverted), and physical presence (Q12: 2% inverted). Q10 is the dominant factor since it directly measures how easily your responsibilities could be redistributed to existing team members. Higher scores mean your work can be easily absorbed by others. Range: [0, 1].
- Senior productivity amplification ($B_{\text{amp}}$): AI only amplifies productivity for work that is both digital and AI-learnable. Raw digitization (Q4) is discounted by factors that make digital work harder for AI to learn from: context dependency (Q7: 35% weight), tacit knowledge (Q9: 30% weight), low decomposability (Q5: 20% weight), and low standardization (Q6: 15% weight). A senior consultant whose deliverables are 100% digital but require extensive context, relationships, and tacit judgment gets minimal amplification. The work is digital, but AI can't learn to replicate it by observing outputs. Conversely, highly digital, standardized, decomposable work with low context enables strong amplification. The boost ranges from 0 to 2.0 (up to +200% output; up to 3× productivity when used in $(1 + B_{\text{amp}})$), scaled by current AI performance (Q1) and job readiness $A_{\text{job}}(t)$. This factor grows over time as AI capability increases.
- Hierarchy vulnerability ($V_{\text{hierarchy}}$): Your position in the workflow determines exposure. Calculated as $(6 - \text{level}) / 5$. Level 1 (many layers above) = 100% vulnerable. Level 4 = 40% vulnerable. Level 5 (top of domain, no one above can do your work) = 20% vulnerable. A principal engineer who owns a system faces minimal compression risk despite being in a "senior" role title.
Parameters differ from full automation: The compression gate opens at $\theta_c = 0.35$ (vs. $\theta \approx 0.50$ for automation), has gentler slope ($\gamma_c = 6.0$ vs. $\gamma = 8.0$), and equal maximum hazard ($h_{\max,c} = 0.40$/year, matching automation's $h_{\max} = 0.40$/year). For vulnerable positions, AI-driven workforce compression through task reallocation poses comparable risk to direct automation. Combined with automation hazard, the total is capped at 0.60/year to reflect real-world institutional friction that prevents instant mass layoffs.
Examples: How the mechanisms interact
High compression risk: Entry-level software engineer
Alex is a junior developer: writing code, fixing bugs, documenting changes. The work is fully digital and breaks into clean pieces. Tickets queue up, code follows established patterns, and most tasks don't require broader organizational knowledge. As AI tools improve, senior engineers absorb Alex's workload. They ship faster with AI assistance, and the backlog of junior-level tickets shrinks.
Alex is at Level 1 with several engineers above who could do this work. Transferable tasks, minimal context needs, and maximum exposure at the bottom of the ladder mean compression kicks in early. Alex's role disappears not because AI replaces it entirely, but because AI-amplified seniors can cover what's left.
Protected: Senior consultant with high context needs
Jordan advises executives on organizational transformation. The deliverables are digital (slides, memos, financial models), but the work runs on tacit knowledge and context. Jordan's recommendations come from pattern recognition across years and industries, reading client politics, and knowing what's unsaid in stakeholder conversations. Each project is different and needs a custom approach.
AI can draft sections and crunch numbers, but it can't replicate judgment built from years of pattern recognition or the relationship intelligence Jordan brings to each engagement. The work is digital but not learnable from outputs alone. Jordan sits at Level 4 with few people above capable of doing this work, and the tasks don't transfer easily. Compression risk is nearly zero. The real threat is full automation much later, when AI develops genuine strategic reasoning. That's a longer horizon than Alex faces.
Moderate risk: Entry-level accountant
Sam processes invoices, reconciles statements, and prepares journal entries at a mid-sized company. The work is mostly digital and somewhat structured, but it isn't fully automated because it needs judgment: matching vendor names that don't quite line up, deciding when to escalate a discrepancy, knowing company-specific account codes. There's context about how the business runs and some unwritten rules about when to bend process.
Sam is at Level 1 with senior accountants and controllers above. As AI improves, those seniors handle more volume. AI helps them process invoices and catch errors faster, so they need less junior support. Sam's work has more context and judgment than Alex's tickets, which slows compression. But it's more learnable than Jordan's consulting, so AI amplification still bites. The result is moderate compression risk that grows with AI capability, though not as fast as it does for the junior engineer.
Re-employment probability
Re-employment odds start at a 60% baseline and adjust based on transferable skills, learning speed, and job performance (0.2 per weighted point). The model subtracts a timing penalty if displacement occurs soon (market saturation makes finding work harder) and applies a hierarchy boost (+0% to +10%). The result clamps between 10% and 85%. No one is guaranteed, but no one is written off.
Timing penalty (graduated scale): If the median technical feasibility hazard occurs within a shorter timeframe, re-employment becomes more difficult due to market saturation. The penalty is a probability reduction applied as follows: median < 3 years: $-0.30$; 3-7 years: $-0.15$; 7-12 years: $-0.05$; >12 years: $0$ (no penalty). This reflects the difficulty of finding alternative employment when many similar roles are being automated simultaneously.
Protection mechanisms (user-actionable):
- Move up hierarchy: reach Level 4–5 (own a domain/system) to reduce compression vulnerability.
- Increase specialization: lower Q10 (make work harder to transfer to others).
- Increase tacit/context: raise Q7 and Q9 (context-dependent, experiential work).
- Reduce digitization overlap: lower Q4 where genuine (hybrid/physical workflows weaken AI amplification).
- Build unique relationships: strengthen Q11/Q12 protective value.
- Strengthen performance: raise Q19 to increase implementation delay and re-employment odds.
Hierarchy levels and seniority effects
Your position in the organizational hierarchy significantly affects both your automation timeline and compression vulnerability. The model defines five hierarchy levels, each with distinct parameter adjustments:
Seniority profile adjustments
Each hierarchy level applies four adjustments to the base model parameters:
- Theta lift ($\Delta\theta$): Adjusts the coverage threshold. Entry-level: -0.02 (automation triggers earlier); Level 5: +0.08 (requires higher AI capability before hazard activates). This reflects that senior roles typically require more comprehensive automation before replacement is viable.
- Hazard shield: Percentage reduction to base hazard rate. Ranges from 0% (Level 1) to 10% (Level 5). Senior roles have more organizational protection and replacement friction.
- Delay shift ($\Delta_{\text{seniority}}$): Adjusts implementation delay. Entry-level: -0.25 years (faster replacement); Level 5: +0.30 years (longer runway). Modified by job performance (Q19).
- Re-employment boost: Multiplier on re-employment probability. Ranges from 1.00× (Level 1) to 1.10× (Level 5). Senior experience improves job market prospects.
Task distribution shifts by seniority
Hierarchy level also shifts your task duration profile. Entry-level roles skew toward shorter, more automatable tasks; senior roles skew toward longer, strategic tasks:
| Level | <10m | 10-45m | 45m-3h | 3-8h | >12h |
| 1 (Entry) | +12% | +8% | -5% | -8% | -7% |
| 2 (Junior) | +5% | +3% | -2% | -3% | -3% |
| 3 (Mid) | 0% | 0% | 0% | 0% | 0% |
| 4 (Senior) | -6% | -4% | +3% | +4% | +3% |
| 5 (Exec) | -12% | -9% | +6% | +8% | +7% |
These shifts are applied to base weights before normalization. Entry-level concentrates work in short tasks; executive level shifts to longer strategic tasks.
The combined effect is substantial: an entry-level role faces earlier automation (lower theta), faster implementation (negative delay shift), higher compression vulnerability (100% hierarchy exposure), and a task profile weighted toward short, easily-automated tasks. A Level 5 executive faces the opposite on all dimensions.
Reading the outputs
The chart shows two survival complements: blue for technical feasibility, green for realized displacement once friction and delay kick in. We integrate $\lambda(s)$ with Simpson's rule, so the area under each curve is the cumulative probability that automation has already happened. Use the controls to stress-test assumptions.
- Median timeline: A binary search finds the year where cumulative probability hits $50\%$. That becomes the headline median job-loss metric.
- Risk by 2030 or 2031: The model calculates years from the current date (when you access the page) to these target years, then evaluates $P_{\text{loss}}$ at that future horizon. For example, accessing the calculator in November 2025 means 2030 is ~4.1 years away. This ensures projections stay relevant as time passes.
- Personal timeline: The $25\%$, $50\%$, $75\%$, and $90\%$ milestones surface when they fall within the next $10$, $15$, $18$, and $25$ years respectively.
- Re-employment label: The probability is bucketed into Good, Moderate, Low, or Very Low for quick scanning, with the precise percentage alongside.
How to work with the model
- Start with the preset that feels closest to your role, then tweak one cluster of questions at a time so you can see which dimensions move the hazard.
- Stress-test the extremes: set AI readiness to five while leaving friction high, then flip it. The distance between those runs is a map of where to invest your energy.
- Pair the re-employment score with the green curve. A fast hazard plus weak re-employment is the trigger for upskilling or a job search; a slow hazard plus strong re-employment buys time for deliberate moves.
Use the weight structure as a checklist: strengthen the protective items you can influence, document the assumptions you cannot, and revisit the calculator as real-world signals shift.
Guide to Advanced Model Tuning
The tuning panel exposes every parameter used in the hazard and compression calculations. Three presets are available at the top of the panel:
- Conservative: Slows capability growth (doubling time 1.3× baseline), raises thresholds (higher theta clamp), lowers the maximum annual automation hazard, smooths the gate, and lengthens implementation delay. Choose this if you expect slow adoption and strong guardrails.
- Baseline: Restores the default configuration derived from METR benchmarks plus the model's transfer and friction assumptions (including the METR-derived doubling time).
- Fast-Takeoff: Speeds capability growth (doubling time 0.7× baseline), lowers thresholds, sharpens the gate, raises the maximum hazard, and shortens delay. Use this to explore aggressive "capability converts to deployment quickly" scenarios.
These presets only set parameter values; you can override any field afterward. They do not change the underlying math, only the assumptions about how quickly capability translates into real-world deployment.